For other posts, visit my Commentary blog
After posting yesterday’s blog titled, “Dolin COVID Model Outperforms Academic and Government Models; Again,” a University of Washington (UW) Professor took exception to my assessment of the UW COVID model’s performance during July. He raised a valid point and so, in the spirit of intellectual discourse, I will address his concerns. But first, let’s summarize yesterday’s critic so we all start at the same place.
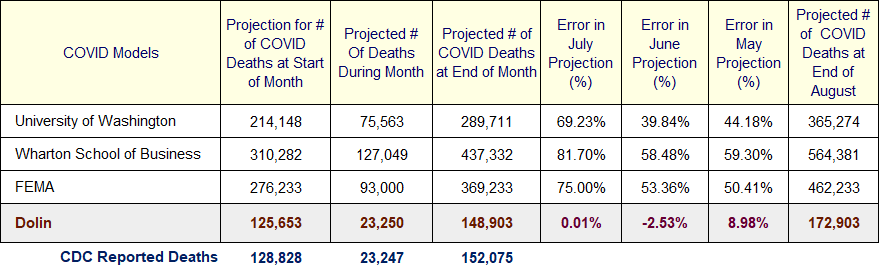
Yesterday I used the above table to assess the performance of the three most referenced COVID models relative to my model, which I refer to as the Dolin Model. The big-three media and White House Coronavirus Task Force models are from the University of Washington, the University of Pennsylvania’s Wharton School of Business and the Government’s Federal Emergency Management Agency (FEMA).
Since early April, I have been tracking projections made by the big-three COVID models. At their best, their error rate was 40% and at their worst the error rate was 82%. The error rate is measured as the delta between each model’s projected number of COVID deaths on a specific date, and the number of deaths that actually occurred by that date, as reported by the CDC. Keep in mind these models, particularly the UW model, were used as the basis for legitimizing government lockdowns and facemask mandates even though their error rates should disqualify them from predicting if the sun will rise tomorrow.
In response to the UW professor’s assertion that pandemic modeling is complicated with a lot of uncertainty, I say, “not really.” While UW no-doubt has a team of dedicated MDs with access to high-powered computers, my model was derived by a single individual on a $200 laptop. Over the three month period of review, my simple model had projection error rates of 0.01%, 2.53% and 9%. Even at it’s worst, the Dolin model significantly outperformed the big-three models. The UW cannot blame their poor performance on COVID’s complexity.
I recognize the difficulty’s in defending an institution that has so consistently performed so poorly, but it is the obligation of scientist to challenge each other’s work to ensure it is of the highest caliber. This is the rational for holding peer reviews prior to publication. UW has a responsibility to hold it’s faculty to rigorous standards and I should not have to lecture senior faculty and administration on this fundamental responsibility. Had UW senior faculty and administration done their job, they would have avoided UW’s current crisis of credibility; even more importantly, it would have thwarted government’s misuse of incorrect projections and prevented the general public’s cascading hysteria. I am unapologetic for doing the work UW was obligated to provide but failed to execute.
The UW professor who took exception to my peer review raises a valid point when he complains that I used the UW model’s upper-tolerance projection for COVID deaths, which was based on their assumption people would not wear facemasks. He suggests that I should have used a lower projection from their tolerance band.
My response to that is two-tiered. First, yes it is true that all numerical models have an error band, or tolerance that’s linked to the uncertainty of input parameters and internal mathematics. This is something I would spend a considerable time discussing with graduate students when I taught Numerical Methods at university. For those unfamiliar, due to the uncertainties involved in modeling an event, such as a pandemic, a scientist will run his/her simulation multiple times using different values for the variables.
If you’ve ever heard of the phrase “Monte Carlo simulation,” it refers to running a simulation thousands of times using every possible combination of viable input parameters and then using statistical analysis of output results to assess which results are most probable. For example, if I model the optimum way to bake an Italian wedding cake, my variables might be oven temperature, batter moisture, size of pan, etc. The output might measure the baking duration and once the model is fine tuned, it would be reasonable to get a projection in the form of “bake 47 minutes plus or minus 1 minute.“
A large error band indicates large uncertainty in your results and an overall lack of confidence. It is important to understand the distinction between simulation results that are possible versus probable (i.e., likely). Suppose in the wedding cake example, your answer was “bake 47 minutes plus or minus 38 minutes.” That would be a meaningless result because the tolerance lacks both precision and accuracy. Is it possible to bake a wedding cake in 9 minutes, yes, but it is probable? It seems this is the state of the UW COVID model, whose tolerance band ranges from “no one dies from COVID” to “365,247 people die by August from COVID.”
Rather than provide a single projection based on the most probable death rate as the Dolin model does, the UW masks their lack of understanding about how to interpret simulation output by implicitly suggesting all results are equally probable depending on the values of input parameters. This is sloppy science and demonstrates a general lack of understanding of numerical methods.
I used to begin my opening lecture in Numerical Methods by presenting students with what I referred to as the “Dolin Fundamental Theorem of Numerical Methods,” which states; “A computer program always gives you an answer.” That theorem was quickly followed by the corollary, “the answer a computer program gives you is always wrong.” From that opening segue, my students and I would spend the rest of the semester delving into how scientist make credible projections from erroneous model simulations. A model projection is only credible when the tolerance band is minimized. The UW model failed to minimize the tolerance band around their projections, which shifts the burden onto me to determine where within their tolerance band to draw a reasonable line in order to assess their results.
The second tier of my response to the UW professor who feels I am being unfair because I base my critic of their performance on the upper end of their tolerance band, I say lets consider that assertion. Based on their own admission, the upper band of the UW model projection is based on people not wearing facemasks. This implies that in order for my assertion that the UW model be assessed relative to the upper tolerance band to be valid, we have to first establish that facemasks are not being worn. I assume we can agree on that.
To start, twenty-two states currently do not require facemasks be worn, some have no facemask regulation and others have suggestions but no formal regulation, they are
- Montana
- Wyoming
- Wisconsin
- South Dakota
- Nevada
- Idaho
- Iowa
- South Carolina
- Arizona
- Alaska
- Indiana
- Minnesota
- Missouri
- New Hampshire
- North Dakota
- Ohio (partial)
- Oklahoma
- Tennessee
- Utah
- Vermont (partial)
- Wisconsin (partial)
- Wyoming
After recently spending a week in Colorado, I can confirm the residents there are not wearing facemasks, which brings the total to twenty-three. Based on media reports, Georgia and Florida residents are also not following mask mandates, which brings the total to twenty-five. New York Governor Cuomo hugs people in public without a mask and NYC mayor DeBlasio says its okay for protestors to not wear masks, which moves our total to twenty-six. Portland and Seattle have relaxed mask wearing for rioters, which moves the total to twenty-eight states with lax to no facemask control, which is over half of the country. If you fold into that other cities that tolerate facemaskless rioters, such as Illinois and California, the lists grows longer
Add to that, the fact that Fauci admits facemasks don’t work and are not a replacement for social distancing. But all fifty states have relaxed their social distancing requirement. Add to that studies that show nonsurgical facemasks, which most people wear, don’t contain the coronavirus. Then add to that the fact that the easiest way for the coronavirus to enter the body is through the eyes, which are not covered, and I think you can see where this is leading. It is reasonable to conclude that the country is not adequately participating in the facemask charade and even if they were, it would not alter the impact of COVID deaths (ala Fauci). So it is reasonable to argue that using the upper tolerance of the UW projection for assessing their model’s performance is not only valid, but responsible.
A final point on this, it is irresponsible to hide under the umbrella of a tolerance band. That’s akin to a modeling the event of flipping a coin and projecting it lands either heads up or heads down, which is totally nonvalue added. The Dolin model, which has been spot on since April, has no tolerance band at all, just a single valued projection. UW’s failure to minimize the tolerance band leaves them open to valid criticism.
I understand how embarrassing and difficult it must be to consider yourself a serious academician at an institution that has shamelessly promoted a poor crisis model while failing to provide adequate peer review. The responsibility, however, was on you and your colleagues at UW to perform a thorough peer review before your medical school blundered their way into national prominence. Is this typical of how UW reviews a doctorial candidate? If so, it would actually explain a lot.
It’s not too late to rectify the embarrassing lack of peer review UW failed to provide and I offer my assistance to help you regain some semblance of academic respectability.
At a time a place of your choosing, I will come and present my COVID model to you and your colleagues for formal peer review. I challenge your medical school to submit to the same simultaneous review, but by scientist not medical professionals. Let’s delve into how each team derived their models and applied them to projections. Let’s unravel the mathematics of each model, as well as each team’s use of input parameters and application of confirmatory analyses. Let’s apply the Dolin Fundamental Law of Numerical Methods to each model and let the chips fall where they may. . . and let’s do this as a live-stream so the country’s entire scientific community can participate. I am up for the scrutiny, is UW?

